Calculate the number of ways to place $n$ rooks on $n \times n$ chessboard so that both following conditions are met:

• each empty cell is under attack;
• exactly $k$ pairs of rooks attack each other.

An empty cell is under attack if there is at least one rook in the same row or at least one rook in the same column. Two rooks attack each other if they share the same row or column, and there are no other rooks between them. For example, there are only two pairs of rooks that attack each other in the following picture:

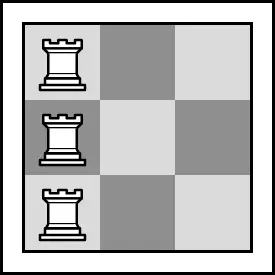
One of the ways to place the rooks for $n = 3$ and $k = 2$ Two ways to place the rooks are considered different if there exists at least one cell which is empty in one of the ways but contains a rook in another way.

The answer might be large, so print it modulo $998244353$ .

Input

The only line of the input contains two integers $n$ and $k$ ( $1 \le n \le 200000$ ; $0 \le k \le \frac{n(n - 1)}{2}$ ).

Output

Print one integer — the number of ways to place the rooks, taken modulo $998244353$ .

Samples

3 2

6

3 3

0

4 0

24

1337 42

807905441