算法一：优先队列（$\Theta(m\log m)$）

首先，容易想到在 $q=0$ 时，我们只需要使用优先队列，每次取出最大的进行分割再放回去即可。

那么当 $q > 0$ 时，考虑怎么处理每次所有蚯蚓共同增加的长度 $q$。我们不可能每次都取出所有元素再一个一个地进行处理。所以我们考虑维护一个偏移量，表示整个集合要共同增加的量，每次取出时先求出原值再操作，然后减去偏移量放回即可。

时间复杂度 $\Theta(m\log m)$。

算法二：普通队列（$\Theta(m)$）

本题中我们还有更加优秀的 $\Theta(m)$ 的做法。

首先考虑 $q=0$ 的情形。这里作出 $p=\dfrac 12$ 时 $\left\lfloor px\right\rfloor$ 和 $x-\left\lfloor px\right\rfloor$ 的图像，会发现它们都是 单调不降 的。

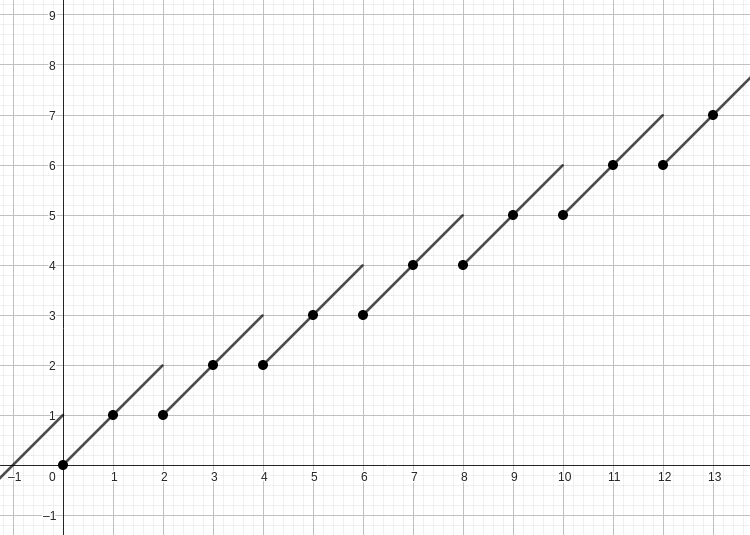
要证：若 $x \leq y$，$0 < p < 1$，则 $\left\lfloor px\right\rfloor \leq \left\lfloor py\right\rfloor$ 且 $x-\left\lfloor px\right\rfloor \leq y-\left\lfloor py\right\rfloor$。

前一个结论易证，而对于后一个结论，易知

$\begin{aligned} & p(y-x) \leq y-x \\ \Rightarrow \ & x-px \leq y-px \\ \Rightarrow \ & \left\lfloor x-px \right\rfloor \leq \left\lfloor y-px \right\rfloor. \\ \end{aligned}$

注意到，$x,\ y$ 是整数，可得

$x - \left\lfloor px \right\rfloor \leq y - \left\lfloor py \right\rfloor.$

证毕。

参考文献：https://www.luogu.com.cn/paste/c4jthmhz（作者：dbxxx）

考虑维护三个队列 $Q,\ Q_1,\ Q_2$。

• 一开始将所有数按照 从大到小 的顺序加入队列 $Q$ 中。

• 每次从三个队列的队头中取最大的弹出，分割成 $\left\lfloor px \right\rfloor$ 和 $x - \left\lfloor px \right\rfloor$ 两段分别加入 $Q_1$ 和 $Q_2$ 的队尾。

• 易知每一步操作结束后三个队列的数都是 单调不增 的，得以保证下一次取出的必然是最大值。

---

再考虑 $q > 0$ 的情况。同样，我们还是维护一个偏移量，但是此时我们需要重新证明上面的结论。

要证：若 $x \leq y$，$0 < p < 1$，则 $\left\lfloor p(x+q)\right\rfloor \leq \left\lfloor py\right\rfloor +q$ 且 $x+q-\left\lfloor p(x+q)\right\rfloor \leq y-\left\lfloor py\right\rfloor+q$。

对于前一个结论，有

$\left\lfloor p(x+q)\right\rfloor = \left\lfloor px+pq\right\rfloor \leq \left\lfloor py+q\right\rfloor = \left\lfloor py\right\rfloor +q.$

对于后一个结论，根据 $q=0$ 时的结论，有

$x+q-\left\lfloor p(x+q)\right\rfloor \leq x-\left\lfloor px\right\rfloor+q \leq y-\left\lfloor py\right\rfloor+q.$

证毕。

时间复杂度 $\Theta(m)$。